밥이되든 죽이되던 프로그래밍
[텅텅머리 시리즈] 1.6. 고윳값과 고유벡터 본문
들어가기전에! "행렬은 선형변환이다"

벡터에 행렬 연산을 취한다는 것
: 행렬을 이용해 벡터를 변환 시켜 주면, 변환 후의 벡터는 변환 전의 벡터와 비교했을 때, 크기도 방향도 모두 변할 수 있다.(선형)
0. 고윳값과 고유벡터의 의미
벡터에 행렬 연산을 취해주면 원래 것과 다른 벡터가 나오는 것이 일반적
하지만, 어떤 벡터들은 선형변환 시 크기만 바뀌고 방향이 바뀌지 않을 수 있음 => 두 벡터가 평행했을 때
벡터 에 선형변환 를 취했을 때, 그 크기만 변하고 원래 벡터와 평행한 벡터 는 무엇인가요?
그렇다면, 그 크기는 얼마나 변했나요?
- 고유벡터(eigenvector): 선형변환 A에 의한 변환 결과가 자기 자신의 상수배가 되는 0이 아닌 벡터
- 고윳값(eigenvalue): 상수배의 값
[DEFINITION]
n x n 정방행렬(고유값, 고유벡터는 정방행렬에 대해서만 정의된다) A에 대해 0이 아닌 솔루션 벡터 가 존재한다면,
를 만족하는 0이 아닌 열벡터 v를 고유벡터, 상수 λ를 고유값이라 정의한다.
좀더 정확한 용어로는 λ는 '행렬 A의 고유값', v는 '행렬 A의 λ에 대한 고유벡터'이다.
즉, 고유값과 고유벡터는 행렬에 따라 정의되는 값으로서 어떤 행렬은 이러한 고유값-고유벡터가 아에 존재하지 않을수도 있고 어떤 행렬은 하나만 존재하거나 또는 최대 n개까지 존재할 수 있다.
고유벡터의 유용성
고유벡터 는 단지 고윳값인 를 곱한 형태이다.
=> A를 곱한 A^2의 고유벡터 또한 x임을 알수 있다.
A(Ax)=A(ㅅx)=ㅅ(Ax)=ㅅ^2x
모든 k=1,2,3, ... 에 대하여 A^kx=ㅅ^kx이고, ㅅ!=0인 ㅅ에 대하여 A-1x=1/ㅅx이다
모든 n차원 벡터 v는 다음과 같이 그 고유벡터들의 일차결합으로 표현된다.
모든 v
A를 곱한 형태
A^k를 곱한 형태
고윳값과 고유벡터의 주요 성질
- S의 대각합: 대각 성분의 합과 고윳갑의 합은 같다
- 행렬식: 행렬식의 값은 고윳값 간 곱과 같다
- 실수 고윳값: 대칭행렬에서 고윳값은 항상실수다
- 직교 고유벡터: 고윳값이 서로 다르면 x_1 x_2=0이다
- 대칭행렬 S는 실수와 비슷하다 => ()
- 직교행렬 Q는 크기가 1인 복소수 ~~와 비슷하다 => ()
- Q의 거듭제곱은 크거나 작아지지 않는다. 왜냐하면, Q의 제곱근들 모두 직교행렬이기 때문이다.
고윳값과 고유벡터, 이것만은 조심하자
- A+B의 고유값은 일반적으로 A 고윳값 + B고윳값과 같지않다
- AB의 고윳값도 마찬가지다
- 중복된 고윳값 ㅅ1, ㅅ2의 경우, 일차독립인 고유벡터가 2개일 것이라는 보장이 없다
- 실수 행렬 A의 고유벡터가 직교하는 것과 AtA=AAt인 것은 동치이다
1. 고윳값 계산 방법

- A-ㅅI 의 역행렬은 존재하지 않는다. => A-ㅅI는 반드시 0이 되어야 한다.
- 이는 ㅅ에 대한 n차 방정식이며, det(A-ㅅI)=0 근은 n개이다.

Q. 만약 A가 A+sI로 평행이동하면, 고유벡터 x와 고유값 ㅅ는 어떻게 될까?
A. 고유벡터 x는 그대로, 모든 고윳값은 s에 의하여 평행이동한다
2) 닮음행렬

닮음인 두 행렬의 고윳값은 같다
모든 가역행렬에 대하여 PAP-1의 고윳값은 B의 고윳값과 같다.
B의 고유벡터 x는 P를 곱한 Px의 형태로 PAP-1의 고유벡터가 된다.
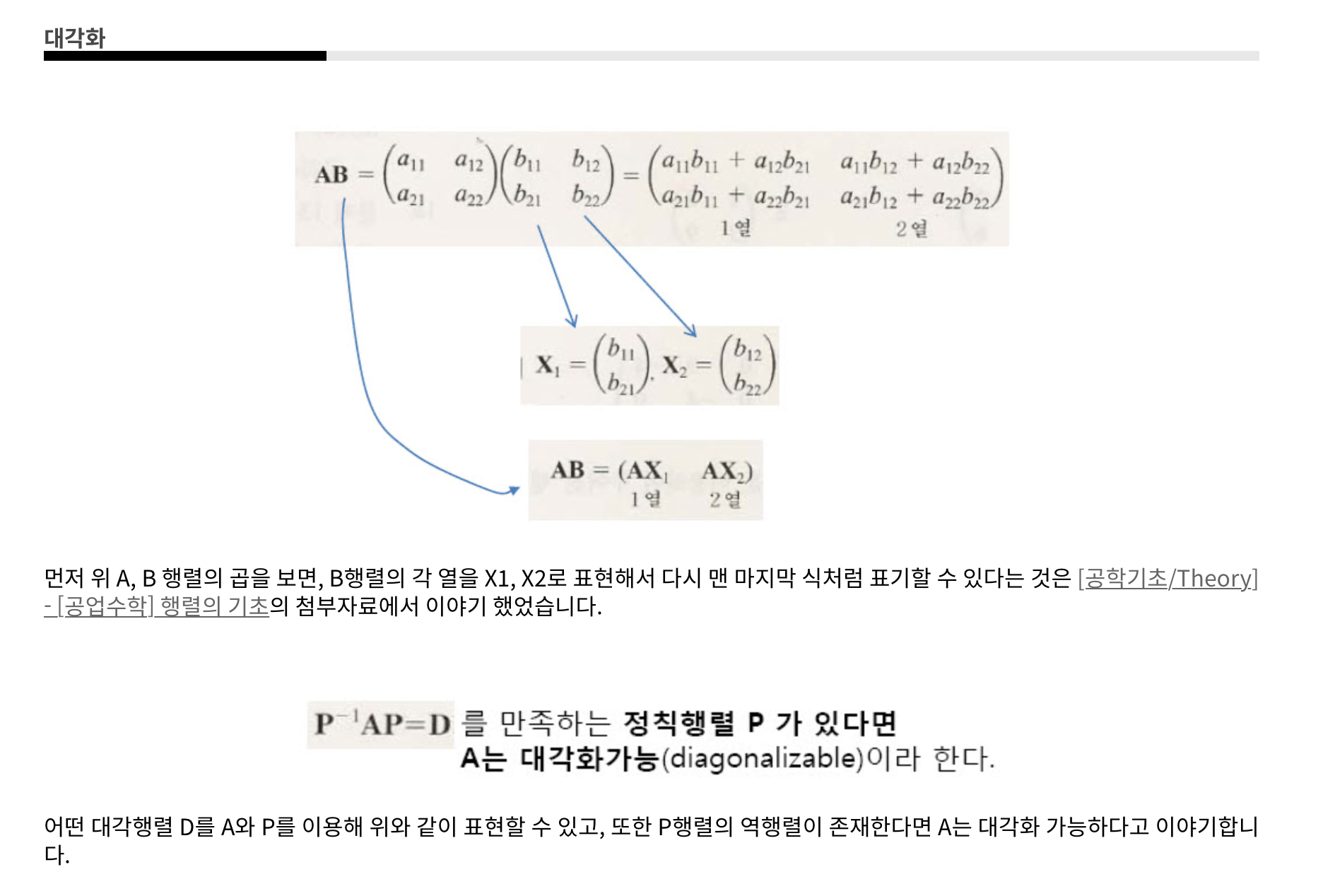
3) 행렬의 대각화
A가 일차독립인 n개의 고유벡터를 가진다고 가정하자.
이 때, 중요한 사실은 행렬이 X와 ㅅ의 곱으로 분해된다는 것이다.
4) 대각화 불가능 행렬
1. 고유벡터: Ax=ㅅx의 0이 아닌 해가 존재한다
2. 고윳값: A-ㅅI의 행렬식은 0이다.
중복도: 수 ㅅ는 단일 고윳값이거나 다중 고윳값이다.
-> 고윳값은 중복도가 M=1dlek.
- 기하적 중복도: ㅅ의 독립인 고유벡터의 갯를 센다
- 대수적 중복도: 고윳값에서 중복되는 ㅅ의 개수를 센다
'DeepLearning > 선형대수로 알아보는 딥러닝' 카테고리의 다른 글
| [텅텅머리 시리즈] 1.8 특잇값 분해에서 특잇값과 특이벡터 (1) | 2022.07.08 |
|---|---|
| [텅텅머리 시리즈]1.7 대칭인 양의 정부호 행렬 (0) | 2022.07.08 |
| [텅텅머리 시리즈] 1.5. 직교행렬과 부분공간 (0) | 2022.07.04 |
| [텅텅머리 시리즈]1.2. Matric Multiplication AB(행렬곱셈) (0) | 2022.07.03 |
| [텅텅머리 시리즈] 1.1. 행렬 A의 열을 이용한 Multiplication Ax (0) | 2022.07.03 |


