밥이되든 죽이되던 프로그래밍
[텅텅머리 시리즈]1.2. Matric Multiplication AB(행렬곱셈) 본문
내적은 AB=C의 각 성분을 계산하는데 필요하다.

각 AB=C의 성분을 계산하는 일반적인 방법은 행렬을 내적하여 원소 하나하나를 multiplication 하는 방식이다. 아래와 같이 나타낼 수 있다;

열과 행의 곱을 통해 행렬곱셈을 나타내는 방법 또한 있다.
- 열 u와 행 v^T를 곱하면 행렬이 만들어진다.
- 행렬 uv^T는 간단하게 나타낼수 있는 행렬이다.
- 외적의 과정으로 볼 수 있다.

Rank가 1인 행렬의 성질

- 행열의 모든 열은 u의 배수이고, 모든 행은 v^T의 배수이다.
- 열공간(column space)는 1차원이다(row space의 차원(일차독립인 열의 개수)은 행렬의 Rank이다)
- 영행렬(zero matric)이 아닌 uv^T는 항상 Rank가 1이고 모든 행렬을 이루는 가장 이상적인 기본 행렬이다.
uv^T의 행공간(row space)는 직선 v를 지나는 직선이다.
행렬 A의 행공간은 행렬 A의 전치행렬 A^T의 열공간 C(A^T)이다.
=> 행벡터, 열벡터를 모두 생각할 필요없이, 열벡터로만 생각해도 된다.
행렬 vu^T를 얻기 위해 uv^T의 전치행렬을 찾으면 된다.
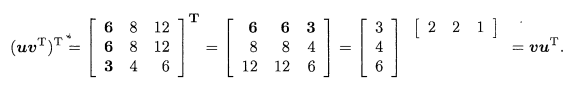
- 행랭크=열랭크, r개의 일차독립 열 <=> r개의 일차독립 행
- 영행렬(zero metric)이 아닌 uv^T에는 각 하나의 일차독립 열과 행이 있다.
1.2.1 AB=(Rank 1 행렬의 합)
다시 행렬 곱셈 AB를 A의 열과 B의 행의 곱셈으로 생각해보자.
a_1 , a_2 , ... , a_n는 A의 n개의 열이라 하고, b*_1, b*_2, ... , b*_n을 B의 n개의 행이라 하자. 이제 행렬 A와 B의 곱 AB는 열 a_k와 행 b*_k의 곱셈의 합이다.
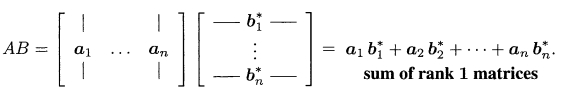
다음은 n=2인 행렬의 합(열과 행의 곱)이 AB가 되는 예이다.

nxn 행렬 A와 B의 곱셈에는 항상 n^3번의 곱셈 연산이 필요하다
- 행 곱하기 열(행렬의 합): mp번의 내적, 매번 n번의 곱셈 => mnp
- 열 곱하기 행(열과 행의 곱): n번의 외적, 매번 mp번의 곱셈 => mnp
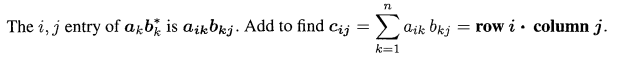
1.2.2 열과 행의 곱셈에 대한 이해
그렇담 외적을 이용한 행렬 곱셈이 데이터 과학에서 필수인 이유는 무엇일까?
행렬에서의 중요한 부분을 찾기 위함이다. 중요한 부분이랑 A의 가장 큰 부분이고, 랭크 1 행렬 uv^T이다.
따라서 선행대수학에서 가장 중요한 주제는 다음과 같다.
A를 CR로 분해하라. 그리고 A=CR의 부분 c_{k}r*_{k}를 살펴보아라
A를 CR로 분해하는 것은 CR=A의 역과정이다.
- 계산에 고윳값 또는 특잇값이 필요하다면 분해하는 데 훨씬 더 오랜 시간이 걸린다
- 고윳값과 특잇값은 행렬의 중요한 정보를 제공한다.
- 그 정보는 행렬을 분해하지 않으면 직접 볼수 없다
5가지 행렬분해
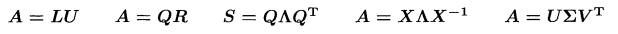
- A=LU : 소거법에서 얻는다.
행의 일차결합으로 A에서 U, U에서 A를 얻을 수 있다.
L은 하삼각행렬, U는 상삼각행렬이다. - A=QR: 그람-슈미트를 통해 열을 직교화하여 얻는다.
Q에 정규직교인 열이 있으며, R은 상삼각행렬이다. - S=QAQ^T: 대칭행렬 S=S^T의 고윳값에서 얻는다.
A의 대각성분은 고윳값이며, Q의 열은 정규직교인 고유벡터이다. - A=XAX^T: 대각화할 수 있다.
대각화는 행렬에 일차독립인 고유벡터가 n개 일때 가능하다 - A=U~V^T: 행렬A의 특잇값 분해(SVD)를 사용한다.
대칭행렬을 활용한 행렬분해
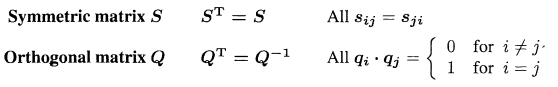
- q_1,...,q_2는 직교단위(orthogonal unit) 고유벡터이다.
- 이 백터들은 서로 직교(내적이 0)하며 Q의 열에 해당한다.
- 대칭행렬 ㅅ의 고윳값은 실수 ㅅ_1,...,ㅅ_n이다.
- 실수 대칭행렬 S에는 n개의 정규직교인 고유벡터 q_1,...,q_n을 가진다
=> 이 벡터를 행렬 S에 곱해도 그 방향은 변하지 않으며, 단지 ㅅ에 의해 크기만 변한다
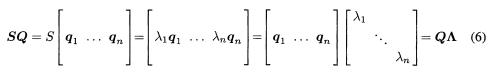
우리의 목적은 SQ=Qㅅ의 각 열을 Sq=ㅅq에서 어떻게 찾는 지 아는 것이다.
=> Q^-1=Q^T이므로 SQ=Qㅅ의 양변에 Q^T를 곱하면 S=QㅅQ^T, 즉 대칭행렬을 얻는다.
- 각 고윳값과 고유벡터는 랭크가 1인 행렬 ㅅ_{k}q_{k}q^{T}_{k}를 만든다.
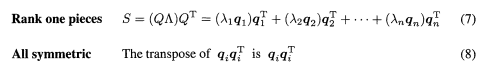
스펙트럼 정리(Spectral Theorem)
'DeepLearning > 선형대수로 알아보는 딥러닝' 카테고리의 다른 글
| [텅텅머리 시리즈] 1.6. 고윳값과 고유벡터 (0) | 2022.07.05 |
|---|---|
| [텅텅머리 시리즈] 1.5. 직교행렬과 부분공간 (0) | 2022.07.04 |
| [텅텅머리 시리즈] 1.1. 행렬 A의 열을 이용한 Multiplication Ax (0) | 2022.07.03 |
| [텅텅머리 시리즈] 1.0. 선형대수학 하이라이트 (0) | 2022.07.03 |
| [선형대수] 텅텅머리 시리즈 LineUp (0) | 2022.07.03 |



